The figure and table below are from Vieth (1999); one of the most widely cited articles on vitamin D. The figure shows the gradual increase in blood concentrations of 25-Hydroxyvitamin, or 25(OH)D, following the start of daily vitamin D3 supplementation of 10,000 IU/day. The table shows the average levels for people living and/or working in sun-rich environments; vitamin D3 is produced by the skin based on sun exposure.
25(OH)D is also referred to as calcidiol. It is a pre-hormone that is produced by the liver based on vitamin D3. To convert from nmol/L to ng/mL, divide by 2.496. The figure suggests that levels start to plateau at around 1 month after the beginning of supplementation, reaching a point of saturation after 2-3 months. Without supplementation or sunlight exposure, levels should go down at a comparable rate. The maximum average level shown on the table is 163 nmol/L (65 ng/mL), and refers to a sample of lifeguards.
From the figure we can infer that people on average will plateau at approximately 130 nmol/L, after months of 10,000 IU/d supplementation. That is 52 ng/mL. Assuming a normal distribution with a standard deviation of about 20 percent of the range of average levels, we can expect about 68 percent of those taking that level of supplementation to be in the 42 to 63 ng/mL range.
This might be the range most of us should expect to be in at an intake of 10,000 IU/d. This is the equivalent to the body’s own natural production through sun exposure.
Approximately 32 percent of the population can be expected to be outside this range. A person who is two standard deviations (SDs) above the mean (i.e., average) would be at around 73 ng/mL. Three SDs above the mean would be 83 ng/mL. Two SDs below the mean would be 31 ng/mL.
There are other factors that may affect levels. For example, being overweight tends to reduce them. Excess cortisol production, from stress, may also reduce them.
Supplementing beyond 10,000 IU/d to reach levels much higher than those in the range of 42 to 63 ng/mL may not be optimal. Interestingly, one cannot overdose through sun exposure, and the idea that people do not produce vitamin D3 after 40 years of age is a myth.
One would be taking in about 14,000 IU/d of vitamin D3 by combining sun exposure with a supplemental dose of 4,000 IU/d. Clear signs of toxicity may not occur until one reaches 50,000 IU/d. Still, one may develop other complications, such as kidney stones, at levels significantly above 10,000 IU/d.
Chris Masterjohn has made a different argument, with somewhat similar conclusions. Chris pointed out that there is a point of saturation above which the liver is unable to properly hydroxylate vitamin D3 to produce 25(OH)D.
How likely it is that a person will develop complications like kidney stones at levels above 10,000 IU/d, and what the danger threshold level could be, are hard to guess. Kidney stone incidence is a sensitive measure of possible problems; but it is, by itself, an unreliable measure. The reason is that it is caused by factors that are correlated with high levels of vitamin D, where those levels may not be the problem.
There is some evidence that kidney stones are associated with living in sunny regions. This is not, in my view, due to high levels of vitamin D3 production from sunlight. Kidney stones are also associated with chronic dehydration, and populations living in sunny regions may be at a higher than average risk of chronic dehydration. This is particularly true for sunny regions that are also very hot and/or dry.
Reference
Vieth, R. (1999). Vitamin D supplementation, 25-hydroxyvitamin D concentrations, and safety. American Journal of Clinical Nutrition, 69(5), 842-856.
Saturday, April 27, 2024
Wednesday, March 27, 2024
The China Study II: Wheat flour, rice, and cardiovascular disease
In another post () on the China Study II, I analyzed the effect of total and HDL cholesterol on mortality from all cardiovascular diseases. The main conclusion was that total and HDL cholesterol were protective. Total and HDL cholesterol usually increase with intake of animal foods, and particularly of animal fat. The lowest mortality from all cardiovascular diseases was in the highest total cholesterol range, 172.5 to 180; and the highest mortality in the lowest total cholesterol range, 120 to 127.5. The difference was quite large; the mortality in the lowest range was approximately 3.3 times higher than in the highest.
This post focuses on the intake of two main plant foods, namely wheat flour and rice intake, and their relationships with mortality from all cardiovascular diseases. After many exploratory multivariate analyses, wheat flour and rice emerged as the plant foods with the strongest associations with mortality from all cardiovascular diseases. Moreover, wheat flour and rice have a strong and inverse relationship with each other, which suggests a “consumption divide”. Since the data is from China in the late 1980s, it is likely that consumption of wheat flour is even higher now. As you’ll see, this picture is alarming.
The main model and results
All of the results reported here are from analyses conducted using WarpPLS (). Below is the model with the main results of the analyses. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore associations between variables, which are shown within ovals. The meaning of each variable is the following: SexM1F2 = sex, with 1 assigned to males and 2 to females; MVASC = mortality from all cardiovascular diseases (ages 35-69); TKCAL = total calorie intake per day; WHTFLOUR = wheat flour intake (g/day); and RICE = and rice intake (g/day).
The variables to the left of MVASC are the main predictors of interest in the model. The one to the right is a control variable – SexM1F2. The path coefficients (indicated as beta coefficients) reflect the strength of the relationships. A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to. The P values indicate the statistical significance of the relationship; a P lower than 0.05 generally means a significant relationship (95 percent or higher likelihood that the relationship is “real”).
In summary, the model above seems to be telling us that:
- As rice intake increases, wheat flour intake decreases significantly (beta=-0.84; P<0.01). This relationship would be the same if the arrow pointed in the opposite direction. It suggests that there is a sharp divide between rice-consuming and wheat flour-consuming regions.
- As wheat flour intake increases, mortality from all cardiovascular diseases increases significantly (beta=0.32; P<0.01). This is after controlling for the effects of rice and total calorie intake. That is, wheat flour seems to have some inherent properties that make it bad for one’s health, even if one doesn’t consume that many calories.
- As rice intake increases, mortality from all cardiovascular diseases decreases significantly (beta=-0.24; P<0.01). This is after controlling for the effects of wheat flour and total calorie intake. That is, this effect is not entirely due to rice being consumed in place of wheat flour. Still, as you’ll see later in this post, this relationship is nonlinear. Excessive rice intake does not seem to be very good for one’s health either.
- Increases in wheat flour and rice intake are significantly associated with increases in total calorie intake (betas=0.25, 0.33; P<0.01). This may be due to wheat flour and rice intake: (a) being themselves, in terms of their own caloric content, main contributors to the total calorie intake; or (b) causing an increase in calorie intake from other sources. The former is more likely, given the effect below.
- The effect of total calorie intake on mortality from all cardiovascular diseases is insignificant when we control for the effects of rice and wheat flour intakes (beta=0.08; P=0.35). This suggests that neither wheat flour nor rice exerts an effect on mortality from all cardiovascular diseases by increasing total calorie intake from other food sources.
- Being female is significantly associated with a reduction in mortality from all cardiovascular diseases (beta=-0.24; P=0.01). This is to be expected. In other words, men are women with a few design flaws, so to speak. (This situation reverses itself a bit after menopause.)
Wheat flour displaces rice
The graph below shows the shape of the association between wheat flour intake (WHTFLOUR) and rice intake (RICE). The values are provided in standardized format; e.g., 0 is the mean (a.k.a. average), 1 is one standard deviation above the mean, and so on. The curve is the best-fitting U curve obtained by the software. It actually has the shape of an exponential decay curve, which can be seen as a section of a U curve. This suggests that wheat flour consumption has strongly displaced rice consumption in several regions in China, and also that wherever rice consumption is high wheat flour consumption tends to be low.
As wheat flour intake goes up, so does cardiovascular disease mortality
The graphs below show the shapes of the association between wheat flour intake (WHTFLOUR) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format; e.g., 0 is the mean (or average), 1 is one standard deviation above the mean, and so on. In the second graph, the values are provided in unstandardized format and organized in terciles (each of three equal intervals).
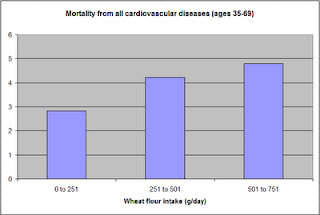
The curve in the first graph is the best-fitting U curve obtained by the software. It is a quasi-linear relationship. The higher the consumption of wheat flour in a county, the higher seems to be the mortality from all cardiovascular diseases. The second graph suggests that mortality in the third tercile, which represents a consumption of wheat flour of 501 to 751 g/day (a lot!), is 69 percent higher than mortality in the first tercile (0 to 251 g/day).
Rice seems to be protective, as long as intake is not too high
The graphs below show the shapes of the association between rice intake (RICE) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format. In the second graph, the values are provided in unstandardized format and organized in terciles.
Here the relationship is more complex. The lowest mortality is clearly in the second tercile (206 to 412 g/day). There is a lot of variation in the first tercile, as suggested by the first graph with the U curve. (Remember, as rice intake goes down, wheat flour intake tends to go up.) The U curve here looks similar to the exponential decay curve shown earlier in the post, for the relationship between rice and wheat flour intake.
In fact, the shape of the association between rice intake and mortality from all cardiovascular diseases looks a bit like an “echo” of the shape of the relationship between rice and wheat flour intake. Here is what is creepy. This echo looks somewhat like the first curve (between rice and wheat flour intake), but with wheat flour intake replaced by “death” (i.e., mortality from all cardiovascular diseases).
What does this all mean?
- Wheat flour displacing rice does not look like a good thing. Wheat flour intake seems to have strongly displaced rice intake in the counties where it is heavily consumed. Generally speaking, that does not seem to have been a good thing. It looks like this is generally associated with increased mortality from all cardiovascular diseases.
- High glycemic index food consumption does not seem to be the problem here. Wheat flour and rice have very similar glycemic indices (but generally not glycemic loads; see below). Both lead to blood glucose and insulin spikes. Yet, rice consumption seems protective when it is not excessive. This is true in part (but not entirely) because it largely displaces wheat flour. Moreover, neither rice nor wheat flour consumption seems to be significantly associated with cardiovascular disease via an increase in total calorie consumption. This is a bit of a blow to the theory that high glycemic carbohydrates necessarily cause obesity, diabetes, and eventually cardiovascular disease.
- The problem with wheat flour is … hard to pinpoint, based on the results summarized here. Maybe it is the fact that it is an ultra-refined carbohydrate-rich food; less refined forms of wheat could be healthier. In fact, the glycemic loads of less refined carbohydrate-rich foods tend to be much lower than those of more refined ones (). (Also, boiled brown rice has a glycemic load that is about three times lower than that of whole wheat bread; whereas the glycemic indices are about the same.) Maybe the problem is wheat flour's gluten content. Maybe it is a combination of various factors (), including these.
Notes
- The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). Whenever nonlinear relationships were modeled, the path coefficients were automatically corrected by the software to account for nonlinearity.
- The software used here identifies non-cyclical and mono-cyclical relationships such as logarithmic, exponential, and hyperbolic decay relationships. Once a relationship is identified, data values are corrected and coefficients calculated. This is not the same as log-transforming data prior to analysis, which is widely used but only works if the underlying relationship is logarithmic. Otherwise, log-transforming data may distort the relationship even more than assuming that it is linear, which is what is done by most statistical software tools.
- The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. In complex and multi-factorial phenomena such as health-related phenomena, many would consider an R-squared of 0.20 as acceptable. Still, such an R-squared would mean that 80 percent of the variance for a particularly variable is unexplained by the data.
- The P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This and other related techniques also tend to yield more reliable results for small samples, and samples with outliers (as long as the outliers are “good” data, and are not the result of measurement error).
- Only two data points per county were used (for males and females). This increased the sample size of the dataset without artificially reducing variance, which is desirable since the dataset is relatively small. This also allowed for the test of commonsense assumptions (e.g., the protective effects of being female), which is always a good idea in a complex analysis because violation of commonsense assumptions may suggest data collection or analysis error. On the other hand, it required the inclusion of a sex variable as a control variable in the analysis, which is no big deal.
- Since all the data was collected around the same time (late 1980s), this analysis assumes a somewhat static pattern of consumption of rice and wheat flour. In other words, let us assume that variations in consumption of a particular food do lead to variations in mortality. Still, that effect will typically take years to manifest itself. This is a major limitation of this dataset and any related analyses.
- Mortality from schistosomiasis infection (MSCHIST) does not confound the results presented here. Only counties where no deaths from schistosomiasis infection were reported have been included in this analysis. Mortality from all cardiovascular diseases (MVASC) was measured using the variable M059 ALLVASCc (ages 35-69).
This post focuses on the intake of two main plant foods, namely wheat flour and rice intake, and their relationships with mortality from all cardiovascular diseases. After many exploratory multivariate analyses, wheat flour and rice emerged as the plant foods with the strongest associations with mortality from all cardiovascular diseases. Moreover, wheat flour and rice have a strong and inverse relationship with each other, which suggests a “consumption divide”. Since the data is from China in the late 1980s, it is likely that consumption of wheat flour is even higher now. As you’ll see, this picture is alarming.
The main model and results
All of the results reported here are from analyses conducted using WarpPLS (). Below is the model with the main results of the analyses. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore associations between variables, which are shown within ovals. The meaning of each variable is the following: SexM1F2 = sex, with 1 assigned to males and 2 to females; MVASC = mortality from all cardiovascular diseases (ages 35-69); TKCAL = total calorie intake per day; WHTFLOUR = wheat flour intake (g/day); and RICE = and rice intake (g/day).
The variables to the left of MVASC are the main predictors of interest in the model. The one to the right is a control variable – SexM1F2. The path coefficients (indicated as beta coefficients) reflect the strength of the relationships. A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to. The P values indicate the statistical significance of the relationship; a P lower than 0.05 generally means a significant relationship (95 percent or higher likelihood that the relationship is “real”).
In summary, the model above seems to be telling us that:
- As rice intake increases, wheat flour intake decreases significantly (beta=-0.84; P<0.01). This relationship would be the same if the arrow pointed in the opposite direction. It suggests that there is a sharp divide between rice-consuming and wheat flour-consuming regions.
- As wheat flour intake increases, mortality from all cardiovascular diseases increases significantly (beta=0.32; P<0.01). This is after controlling for the effects of rice and total calorie intake. That is, wheat flour seems to have some inherent properties that make it bad for one’s health, even if one doesn’t consume that many calories.
- As rice intake increases, mortality from all cardiovascular diseases decreases significantly (beta=-0.24; P<0.01). This is after controlling for the effects of wheat flour and total calorie intake. That is, this effect is not entirely due to rice being consumed in place of wheat flour. Still, as you’ll see later in this post, this relationship is nonlinear. Excessive rice intake does not seem to be very good for one’s health either.
- Increases in wheat flour and rice intake are significantly associated with increases in total calorie intake (betas=0.25, 0.33; P<0.01). This may be due to wheat flour and rice intake: (a) being themselves, in terms of their own caloric content, main contributors to the total calorie intake; or (b) causing an increase in calorie intake from other sources. The former is more likely, given the effect below.
- The effect of total calorie intake on mortality from all cardiovascular diseases is insignificant when we control for the effects of rice and wheat flour intakes (beta=0.08; P=0.35). This suggests that neither wheat flour nor rice exerts an effect on mortality from all cardiovascular diseases by increasing total calorie intake from other food sources.
- Being female is significantly associated with a reduction in mortality from all cardiovascular diseases (beta=-0.24; P=0.01). This is to be expected. In other words, men are women with a few design flaws, so to speak. (This situation reverses itself a bit after menopause.)
Wheat flour displaces rice
The graph below shows the shape of the association between wheat flour intake (WHTFLOUR) and rice intake (RICE). The values are provided in standardized format; e.g., 0 is the mean (a.k.a. average), 1 is one standard deviation above the mean, and so on. The curve is the best-fitting U curve obtained by the software. It actually has the shape of an exponential decay curve, which can be seen as a section of a U curve. This suggests that wheat flour consumption has strongly displaced rice consumption in several regions in China, and also that wherever rice consumption is high wheat flour consumption tends to be low.
As wheat flour intake goes up, so does cardiovascular disease mortality
The graphs below show the shapes of the association between wheat flour intake (WHTFLOUR) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format; e.g., 0 is the mean (or average), 1 is one standard deviation above the mean, and so on. In the second graph, the values are provided in unstandardized format and organized in terciles (each of three equal intervals).
The curve in the first graph is the best-fitting U curve obtained by the software. It is a quasi-linear relationship. The higher the consumption of wheat flour in a county, the higher seems to be the mortality from all cardiovascular diseases. The second graph suggests that mortality in the third tercile, which represents a consumption of wheat flour of 501 to 751 g/day (a lot!), is 69 percent higher than mortality in the first tercile (0 to 251 g/day).
Rice seems to be protective, as long as intake is not too high
The graphs below show the shapes of the association between rice intake (RICE) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format. In the second graph, the values are provided in unstandardized format and organized in terciles.
Here the relationship is more complex. The lowest mortality is clearly in the second tercile (206 to 412 g/day). There is a lot of variation in the first tercile, as suggested by the first graph with the U curve. (Remember, as rice intake goes down, wheat flour intake tends to go up.) The U curve here looks similar to the exponential decay curve shown earlier in the post, for the relationship between rice and wheat flour intake.
In fact, the shape of the association between rice intake and mortality from all cardiovascular diseases looks a bit like an “echo” of the shape of the relationship between rice and wheat flour intake. Here is what is creepy. This echo looks somewhat like the first curve (between rice and wheat flour intake), but with wheat flour intake replaced by “death” (i.e., mortality from all cardiovascular diseases).
What does this all mean?
- Wheat flour displacing rice does not look like a good thing. Wheat flour intake seems to have strongly displaced rice intake in the counties where it is heavily consumed. Generally speaking, that does not seem to have been a good thing. It looks like this is generally associated with increased mortality from all cardiovascular diseases.
- High glycemic index food consumption does not seem to be the problem here. Wheat flour and rice have very similar glycemic indices (but generally not glycemic loads; see below). Both lead to blood glucose and insulin spikes. Yet, rice consumption seems protective when it is not excessive. This is true in part (but not entirely) because it largely displaces wheat flour. Moreover, neither rice nor wheat flour consumption seems to be significantly associated with cardiovascular disease via an increase in total calorie consumption. This is a bit of a blow to the theory that high glycemic carbohydrates necessarily cause obesity, diabetes, and eventually cardiovascular disease.
- The problem with wheat flour is … hard to pinpoint, based on the results summarized here. Maybe it is the fact that it is an ultra-refined carbohydrate-rich food; less refined forms of wheat could be healthier. In fact, the glycemic loads of less refined carbohydrate-rich foods tend to be much lower than those of more refined ones (). (Also, boiled brown rice has a glycemic load that is about three times lower than that of whole wheat bread; whereas the glycemic indices are about the same.) Maybe the problem is wheat flour's gluten content. Maybe it is a combination of various factors (), including these.
Notes
- The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). Whenever nonlinear relationships were modeled, the path coefficients were automatically corrected by the software to account for nonlinearity.
- The software used here identifies non-cyclical and mono-cyclical relationships such as logarithmic, exponential, and hyperbolic decay relationships. Once a relationship is identified, data values are corrected and coefficients calculated. This is not the same as log-transforming data prior to analysis, which is widely used but only works if the underlying relationship is logarithmic. Otherwise, log-transforming data may distort the relationship even more than assuming that it is linear, which is what is done by most statistical software tools.
- The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. In complex and multi-factorial phenomena such as health-related phenomena, many would consider an R-squared of 0.20 as acceptable. Still, such an R-squared would mean that 80 percent of the variance for a particularly variable is unexplained by the data.
- The P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This and other related techniques also tend to yield more reliable results for small samples, and samples with outliers (as long as the outliers are “good” data, and are not the result of measurement error).
- Only two data points per county were used (for males and females). This increased the sample size of the dataset without artificially reducing variance, which is desirable since the dataset is relatively small. This also allowed for the test of commonsense assumptions (e.g., the protective effects of being female), which is always a good idea in a complex analysis because violation of commonsense assumptions may suggest data collection or analysis error. On the other hand, it required the inclusion of a sex variable as a control variable in the analysis, which is no big deal.
- Since all the data was collected around the same time (late 1980s), this analysis assumes a somewhat static pattern of consumption of rice and wheat flour. In other words, let us assume that variations in consumption of a particular food do lead to variations in mortality. Still, that effect will typically take years to manifest itself. This is a major limitation of this dataset and any related analyses.
- Mortality from schistosomiasis infection (MSCHIST) does not confound the results presented here. Only counties where no deaths from schistosomiasis infection were reported have been included in this analysis. Mortality from all cardiovascular diseases (MVASC) was measured using the variable M059 ALLVASCc (ages 35-69).
Labels:
cardiovascular disease,
China Study,
multivariate analysis,
research,
rice,
statistics,
warppls,
wheat
Thursday, February 29, 2024
The lowest-mortality BMI: What is the role of nutrient intake from food?
In a previous post (), I discussed the frequently reported lowest-mortality body mass index (BMI), which is about 26. The empirical results reviewed in that post suggest that fat-free mass plays an important role in that context. Keep in mind that this "BMI=26 phenomenon" is often reported in studies of populations from developed countries, which are likely to be relatively sedentary. This is important for the point made in this post.
A lowest-mortality BMI of 26 is somehow at odds with the fact that many healthy and/or long-living populations have much lower BMIs. You can clearly see this in the distribution of BMIs among males in Kitava and Sweden shown in the graph below, from a study by Lindeberg and colleagues (). This distribution is shifted in such a way that would suggest a much lower BMI of lowest-mortality among the Kitavans, assuming a U-curve shape similar to that observed in studies of populations from developed countries ().
Another relevant example comes from the China Study II (see, e.g., ), which is based on data from 8000 adults. The average BMI in the China Study II dataset, with data from the 1980s, is approximately 21; for an average weight that is about 116 lbs. That BMI is relatively uniform across Chinese counties, including those with the lowest mortality rates. No county has an average BMI that is 26; not even close. This also supports the idea that Chinese people were, at least during that period, relatively thin.
Now take a look at the graph below, also based on the China Study II dataset, from a previous post (), relating total daily calorie intake with longevity. I should note that the relationship between total daily calorie intake and longevity depicted in this graph is not really statistically significant. Still, the highest longevity seems to be in the second tercile of total daily calorie intake.
Again, the average weight in the dataset is about 116 lbs. A conservative estimate of the number of calories needed to maintain this weight without any physical activity would be about 1740. Add about 700 calories to that, for a reasonable and healthy level of physical activity, and you get 2440 calories needed daily for weight maintenance. That is right in the middle of the second tercile, the one with the highest longevity.
What does this have to do with the lowest-mortality BMI of 26 from studies of samples from developed countries? Populations in these countries are likely to be relatively sedentary, at least on average, in which case a low BMI will be associated with a low total calorie intake. And a low total calorie intake will lead to a low intake of nutrients needed by the body to fight disease.
And don’t think you can fix this problem by consuming lots of vitamin and mineral pills. When I refer here to a higher or lower nutrient intake, I am not talking only about micronutrients, but also about macronutrients (fatty and amino acids) in amounts that are needed by your body. Moreover, important micronutrients, such as fat-soluble vitamins, cannot be properly absorbed without certain macronutrients, such as fat.
Industrial nutrient isolation for supplementation use has not been a very successful long-term strategy for health optimization (). On the other hand, this type of supplementation has indeed been found to have had modest-to-significant success in short-term interventions aimed at correcting acute health problems caused by severe nutritional deficiencies ().
So the "BMI=26 phenomenon" may be a reflection not of a direct effect of high muscularity on health, but of an indirect effect mediated by a high intake of needed nutrients among sedentary folks. This may be so even though the lowest mortality is for the combination of that BMI with a relatively small waist (), which suggests some level of muscularity, but not necessarily serious bodybuilder-level muscularity. High muscularity, of the serious bodybuilder type, is not very common; at least not enough to significantly sway results based on the analysis of large samples.
The combination of a BMI=26 with a relatively small waist is indicative of more muscle and less body fat. Having more muscle and less body fat has an advantage that is rarely discussed. It allows for a higher total calorie intake, and thus a higher nutrient intake, without an unhealthy increase in body fat. Muscle mass increases one's caloric requirement for weight maintenance, more so than body fat. Body fat also increases that caloric requirement, but it also acts like an organ, secreting a number of hormones into the bloodstream, and becoming pro-inflammatory in an unhealthy way above a certain level.
Clearly having a low body fat percentage is associated with lower incidence of degenerative diseases, but it will likely lead to a lower intake of nutrients relative to one’s needs unless other factors are present, e.g., being fairly muscular or physically active. Chronic low nutrient intake tends to get people closer to the afterlife like nothing else ().
In this sense, having a BMI=26 and being relatively sedentary (without being skinny-fat) has an effect that is similar to that of having a BMI=21 and being fairly physically active. Both would lead to consumption of more calories for weight maintenance, and thus more nutrients, as long as nutritious foods are eaten.
A lowest-mortality BMI of 26 is somehow at odds with the fact that many healthy and/or long-living populations have much lower BMIs. You can clearly see this in the distribution of BMIs among males in Kitava and Sweden shown in the graph below, from a study by Lindeberg and colleagues (). This distribution is shifted in such a way that would suggest a much lower BMI of lowest-mortality among the Kitavans, assuming a U-curve shape similar to that observed in studies of populations from developed countries ().
Another relevant example comes from the China Study II (see, e.g., ), which is based on data from 8000 adults. The average BMI in the China Study II dataset, with data from the 1980s, is approximately 21; for an average weight that is about 116 lbs. That BMI is relatively uniform across Chinese counties, including those with the lowest mortality rates. No county has an average BMI that is 26; not even close. This also supports the idea that Chinese people were, at least during that period, relatively thin.
Now take a look at the graph below, also based on the China Study II dataset, from a previous post (), relating total daily calorie intake with longevity. I should note that the relationship between total daily calorie intake and longevity depicted in this graph is not really statistically significant. Still, the highest longevity seems to be in the second tercile of total daily calorie intake.
Again, the average weight in the dataset is about 116 lbs. A conservative estimate of the number of calories needed to maintain this weight without any physical activity would be about 1740. Add about 700 calories to that, for a reasonable and healthy level of physical activity, and you get 2440 calories needed daily for weight maintenance. That is right in the middle of the second tercile, the one with the highest longevity.
What does this have to do with the lowest-mortality BMI of 26 from studies of samples from developed countries? Populations in these countries are likely to be relatively sedentary, at least on average, in which case a low BMI will be associated with a low total calorie intake. And a low total calorie intake will lead to a low intake of nutrients needed by the body to fight disease.
And don’t think you can fix this problem by consuming lots of vitamin and mineral pills. When I refer here to a higher or lower nutrient intake, I am not talking only about micronutrients, but also about macronutrients (fatty and amino acids) in amounts that are needed by your body. Moreover, important micronutrients, such as fat-soluble vitamins, cannot be properly absorbed without certain macronutrients, such as fat.
Industrial nutrient isolation for supplementation use has not been a very successful long-term strategy for health optimization (). On the other hand, this type of supplementation has indeed been found to have had modest-to-significant success in short-term interventions aimed at correcting acute health problems caused by severe nutritional deficiencies ().
So the "BMI=26 phenomenon" may be a reflection not of a direct effect of high muscularity on health, but of an indirect effect mediated by a high intake of needed nutrients among sedentary folks. This may be so even though the lowest mortality is for the combination of that BMI with a relatively small waist (), which suggests some level of muscularity, but not necessarily serious bodybuilder-level muscularity. High muscularity, of the serious bodybuilder type, is not very common; at least not enough to significantly sway results based on the analysis of large samples.
The combination of a BMI=26 with a relatively small waist is indicative of more muscle and less body fat. Having more muscle and less body fat has an advantage that is rarely discussed. It allows for a higher total calorie intake, and thus a higher nutrient intake, without an unhealthy increase in body fat. Muscle mass increases one's caloric requirement for weight maintenance, more so than body fat. Body fat also increases that caloric requirement, but it also acts like an organ, secreting a number of hormones into the bloodstream, and becoming pro-inflammatory in an unhealthy way above a certain level.
Clearly having a low body fat percentage is associated with lower incidence of degenerative diseases, but it will likely lead to a lower intake of nutrients relative to one’s needs unless other factors are present, e.g., being fairly muscular or physically active. Chronic low nutrient intake tends to get people closer to the afterlife like nothing else ().
In this sense, having a BMI=26 and being relatively sedentary (without being skinny-fat) has an effect that is similar to that of having a BMI=21 and being fairly physically active. Both would lead to consumption of more calories for weight maintenance, and thus more nutrients, as long as nutritious foods are eaten.
Sunday, January 28, 2024
Looking for a good orthodontist? My recommendation is Dr. Meat
The figure below is one of many in Weston Price’s outstanding book Nutrition and Physical Degeneration showing evidence of teeth crowding among children whose parents moved from a traditional diet of minimally processed foods to a Westernized diet. ()
Tooth crowding and other forms of malocclusion are widespread and on the rise in populations that have adopted Westernized diets (most of us). Some blame it on dental caries, particularly in early childhood; dental caries are also a hallmark of Westernized diets. Varrela, however, in a study of Finnish skulls from the 15th and 16th centuries found evidence of dental caries, but not of malocclusion, which Varrela reported as fairly high in modern Finns. ()
Why does malocclusion occur at all in the context of Westernized diets? Lombardi () put forth an evolutionary hypothesis:
So what is one to do? Apparently getting babies to eat meat is not a bad idea (). They may well just chew on it for a while and spit it out. The likelihood of meat inducing dental caries is very low, as most low carbers can attest. (In fact, low carbers who eat mostly meat often see dental caries heal.)
Concerned about the baby choking on meat? See this Google search for “baby choked on meat”: (). Now, see this Google search for “baby choked on milk”: ().
What if you have a child with crowded teeth as a preteen or teen? Too late? Should you get him or her to use “cute” braces? Our daughter had crowded teeth as a preteen. It overlapped with the period of my transformation (), which meant that she started having a lot more natural foods to eat. There were more of those around, some of which require serious chewing, and less industrialized soft foods. Those natural foods included hard-to-chew beef cuts, served multiple times a week.
We noticed improvement right away, and in a few years the crowding disappeared. Soon she had the kind of smile that could land her a job as a toothpaste model:
The key seems to be to start early, in developmental years. If you are an adult with crowded teeth, malocclusion may not be solved by either tough foods or braces. With braces, you may even end up with other problems ().
Tooth crowding and other forms of malocclusion are widespread and on the rise in populations that have adopted Westernized diets (most of us). Some blame it on dental caries, particularly in early childhood; dental caries are also a hallmark of Westernized diets. Varrela, however, in a study of Finnish skulls from the 15th and 16th centuries found evidence of dental caries, but not of malocclusion, which Varrela reported as fairly high in modern Finns. ()
Why does malocclusion occur at all in the context of Westernized diets? Lombardi () put forth an evolutionary hypothesis:
“In modern man there is little attrition of the teeth because of a soft, processed diet; this can result in dental crowding and impaction of the third molars. It is postulated that the tooth-jaw size discrepancy apparent in modern man as dental crowding is, in primitive man, a crucial biologic adaptation imposed by the selection pressures of a demanding diet that maintains sufficient chewing surface area for long-term survival. Selection pressures for teeth large enough to withstand a rigorous diet have been relaxed only recently in advanced populations, and the slow pace of evolutionary change has not yet brought the teeth and jaws into harmonious relationship.”
So what is one to do? Apparently getting babies to eat meat is not a bad idea (). They may well just chew on it for a while and spit it out. The likelihood of meat inducing dental caries is very low, as most low carbers can attest. (In fact, low carbers who eat mostly meat often see dental caries heal.)
Concerned about the baby choking on meat? See this Google search for “baby choked on meat”: (). Now, see this Google search for “baby choked on milk”: ().
What if you have a child with crowded teeth as a preteen or teen? Too late? Should you get him or her to use “cute” braces? Our daughter had crowded teeth as a preteen. It overlapped with the period of my transformation (), which meant that she started having a lot more natural foods to eat. There were more of those around, some of which require serious chewing, and less industrialized soft foods. Those natural foods included hard-to-chew beef cuts, served multiple times a week.
We noticed improvement right away, and in a few years the crowding disappeared. Soon she had the kind of smile that could land her a job as a toothpaste model:
The key seems to be to start early, in developmental years. If you are an adult with crowded teeth, malocclusion may not be solved by either tough foods or braces. With braces, you may even end up with other problems ().
Labels:
braces,
dental caries,
malocclusion,
my experience,
research
Wednesday, December 27, 2023
We share an ancestor who probably lived no more than 640 years ago
We all evolved from one single-celled organism that lived billions of years ago. I don’t see why this is so hard for some people to believe, given that all of us also developed from a single fertilized cell in just 9 months.
However, our most recent common ancestor is not that first single-celled organism, nor is it the first Homo sapiens, or even the first Cro-Magnon.
The majority of the people who read this blog probably share a common ancestor who lived no more than 640 years ago. Genealogical records often reveal interesting connections - the figure below has been cropped from a larger one from Pinterest.
You and I, whoever you are, have each two parents. Each of our parents have (or had) two parents, who themselves had two parents. And so on.
If we keep going back in time, and assume that you and I do not share a common ancestor, there will be a point where the theoretical world population would have to be impossibly large.
Assuming a new generation coming up every 20 years, and going backwards in time, we get a theoretical population chart like the one below. The theoretical population grows in an exponential, or geometric, fashion.
As we move back in time the bars go up in size. Beyond a certain point their sizes go up so fast that you have to segment the chart. Otherwise the bars on the left side of the chart disappear in comparison to the ones on the right side (as several did on the chart above). Below is the section of the chart going back to the year 1371.
The year 1371 is a little more than 640 years ago. (This post is revised from another dated a few years ago, hence the number 640.) And what is the theoretical population in that year if we assume that you and I have no common ancestors? The answer is: more than 8.5 billion people. We know that is not true.
Admittedly this is a somewhat simplistic view of this phenomenon, used here primarily to make a point. For example, it is possible that a population of humans became isolated 15 thousand years ago, remained isolated to the present day, and that one of their descendants just happened to be around reading this blog today.
Perhaps the most widely cited article discussing this idea is this one by Joseph T. Chang, published in the journal Advances in Applied Probability. For a more accessible introduction to the idea, see this article by Joe Kissell.
Estimates vary based on the portion of the population considered. There are also assumptions that have to be made based on migration and mating patterns, as well as the time for each generation to emerge and the stability of that number over time.
Still, most people alive today share a common ancestor who lived a lot more recently than they think. In most cases that common ancestor probably lived less than 640 years ago.
And who was that common ancestor? That person was probably a man who, due to a high perceived social status, had many consorts, who gave birth to many children. Someone like Genghis Khan.
However, our most recent common ancestor is not that first single-celled organism, nor is it the first Homo sapiens, or even the first Cro-Magnon.
The majority of the people who read this blog probably share a common ancestor who lived no more than 640 years ago. Genealogical records often reveal interesting connections - the figure below has been cropped from a larger one from Pinterest.
You and I, whoever you are, have each two parents. Each of our parents have (or had) two parents, who themselves had two parents. And so on.
If we keep going back in time, and assume that you and I do not share a common ancestor, there will be a point where the theoretical world population would have to be impossibly large.
Assuming a new generation coming up every 20 years, and going backwards in time, we get a theoretical population chart like the one below. The theoretical population grows in an exponential, or geometric, fashion.
As we move back in time the bars go up in size. Beyond a certain point their sizes go up so fast that you have to segment the chart. Otherwise the bars on the left side of the chart disappear in comparison to the ones on the right side (as several did on the chart above). Below is the section of the chart going back to the year 1371.
The year 1371 is a little more than 640 years ago. (This post is revised from another dated a few years ago, hence the number 640.) And what is the theoretical population in that year if we assume that you and I have no common ancestors? The answer is: more than 8.5 billion people. We know that is not true.
Admittedly this is a somewhat simplistic view of this phenomenon, used here primarily to make a point. For example, it is possible that a population of humans became isolated 15 thousand years ago, remained isolated to the present day, and that one of their descendants just happened to be around reading this blog today.
Perhaps the most widely cited article discussing this idea is this one by Joseph T. Chang, published in the journal Advances in Applied Probability. For a more accessible introduction to the idea, see this article by Joe Kissell.
Estimates vary based on the portion of the population considered. There are also assumptions that have to be made based on migration and mating patterns, as well as the time for each generation to emerge and the stability of that number over time.
Still, most people alive today share a common ancestor who lived a lot more recently than they think. In most cases that common ancestor probably lived less than 640 years ago.
And who was that common ancestor? That person was probably a man who, due to a high perceived social status, had many consorts, who gave birth to many children. Someone like Genghis Khan.
Labels:
evolution,
genetics,
recent common ancestor,
research,
statistics
Sunday, November 26, 2023
Subcutaneous versus visceral fat: How to tell the difference?
The photos below, from Wikipedia, show two patterns of abdominal fat deposition. The one on the left is predominantly of subcutaneous abdominal fat deposition. The one on the right is an example of visceral abdominal fat deposition, around internal organs, together with a significant amount of subcutaneous fat deposition as well.
Body fat is not an inert mass used only to store energy. Body fat can be seen as a “distributed organ”, as it secretes a number of hormones into the bloodstream. For example, it secretes leptin, which regulates hunger. It secretes adiponectin, which has many health-promoting properties. It also secretes tumor necrosis factor-alpha (more recently referred to as simply “tumor necrosis factor” in the medical literature), which promotes inflammation. Inflammation is necessary to repair damaged tissue and deal with pathogens, but too much of it does more harm than good.
How does one differentiate subcutaneous from visceral abdominal fat?
Subcutaneous abdominal fat shifts position more easily as one’s body moves. When one is standing, subcutaneous fat often tends to fold around the navel, creating a “mouth” shape. Subcutaneous fat is easier to hold in one’s hand, as shown on the left photo above. Because subcutaneous fat tends to “shift” more easily as one changes the position of the body, if you measure your waist circumference lying down and standing up, and the difference is large (a one-inch difference can be considered large), you probably have a significant amount of subcutaneous fat.
Waist circumference is a variable that reflects individual changes in body fat percentage fairly well. This is especially true as one becomes lean (e.g., around 14-17 percent or less of body fat for men, and 21-24 for women), because as that happens abdominal fat contributes to an increasingly higher proportion of total body fat. For people who are lean, a 1-inch reduction in waist circumference will frequently translate into a 2-3 percent reduction in body fat percentage. Having said that, waist circumference comparisons between individuals are often misleading. Waist-to-fat ratios tend to vary a lot among different individuals (like almost any trait). This means that someone with a 34-inch waist (measured at the navel) may have a lower body fat percentage than someone with a 33-inch waist.
Subcutaneous abdominal fat is hard to mobilize; that is, it is hard to burn through diet and exercise. This is why it is often called the “stubborn” abdominal fat. One reason for the difficulty in mobilizing subcutaneous abdominal fat is that the network of blood vessels is not as dense in the area where this type of fat occurs, as it is with visceral fat. Another reason, which is related to degree of vascularization, is that subcutaneous fat is farther away from the portal vein than visceral fat. As such, it has to travel a longer distance to reach the main “highway” that will take it to other tissues (e.g., muscle) for use as energy.
In terms of health, excess subcutaneous fat is not nearly as detrimental as excess visceral fat. Excess visceral fat typically happens together with excess subcutaneous fat; but not necessarily the other way around. For instance, sumo wrestlers frequently have excess subcutaneous fat, but little or no visceral fat. The more health-detrimental effect of excess visceral fat is probably related to its proximity to the portal vein, which amplifies the negative health effects of excessive pro-inflammatory hormone secretion. Those hormones reach a major transport “highway” rather quickly.
Even though excess subcutaneous body fat is more benign than excess visceral fat, excess body fat of any kind is unlikely to be health-promoting. From an evolutionary perspective, excess body fat impaired agile movement and decreased circulating adiponectin levels; the latter leading to a host of negative health effects. In modern humans, negative health effects may be much less pronounced with subcutaneous than visceral fat, but they will still occur.
Based on studies of isolated hunger-gatherers, it is reasonable to estimate “natural” body fat levels among our Stone Age ancestors, and thus optimal body fat levels in modern humans, to be around 6-13 percent in men and 14–20 percent in women.
If you think that being overweight probably protected some of our Stone Age ancestors during times of famine, here is one interesting factoid to consider. It will take over a month for a man weighing 150 lbs and with 10 percent body fat to die from starvation, and death will not be typically caused by too little body fat being left for use as a source of energy. In starvation, normally death will be caused by heart failure, as the body slowly breaks down muscle tissue (including heart muscle) to maintain blood glucose levels.
References:
Arner, P. (2005). Site differences in human subcutaneous adipose tissue metabolism in obesity. Aesthetic Plastic Surgery, 8(1), 13-17.
Brooks, G.A., Fahey, T.D., & Baldwin, K.M. (2005). Exercise physiology: Human bioenergetics and its applications. Boston, MA: McGraw-Hill.
Fleck, S.J., & Kraemer, W.J. (2004). Designing resistance training programs. Champaign, IL: Human Kinetics.
Taubes, G. (2007). Good calories, bad calories: Challenging the conventional wisdom on diet, weight control, and disease. New York, NY: Alfred A. Knopf.
Body fat is not an inert mass used only to store energy. Body fat can be seen as a “distributed organ”, as it secretes a number of hormones into the bloodstream. For example, it secretes leptin, which regulates hunger. It secretes adiponectin, which has many health-promoting properties. It also secretes tumor necrosis factor-alpha (more recently referred to as simply “tumor necrosis factor” in the medical literature), which promotes inflammation. Inflammation is necessary to repair damaged tissue and deal with pathogens, but too much of it does more harm than good.
How does one differentiate subcutaneous from visceral abdominal fat?
Subcutaneous abdominal fat shifts position more easily as one’s body moves. When one is standing, subcutaneous fat often tends to fold around the navel, creating a “mouth” shape. Subcutaneous fat is easier to hold in one’s hand, as shown on the left photo above. Because subcutaneous fat tends to “shift” more easily as one changes the position of the body, if you measure your waist circumference lying down and standing up, and the difference is large (a one-inch difference can be considered large), you probably have a significant amount of subcutaneous fat.
Waist circumference is a variable that reflects individual changes in body fat percentage fairly well. This is especially true as one becomes lean (e.g., around 14-17 percent or less of body fat for men, and 21-24 for women), because as that happens abdominal fat contributes to an increasingly higher proportion of total body fat. For people who are lean, a 1-inch reduction in waist circumference will frequently translate into a 2-3 percent reduction in body fat percentage. Having said that, waist circumference comparisons between individuals are often misleading. Waist-to-fat ratios tend to vary a lot among different individuals (like almost any trait). This means that someone with a 34-inch waist (measured at the navel) may have a lower body fat percentage than someone with a 33-inch waist.
Subcutaneous abdominal fat is hard to mobilize; that is, it is hard to burn through diet and exercise. This is why it is often called the “stubborn” abdominal fat. One reason for the difficulty in mobilizing subcutaneous abdominal fat is that the network of blood vessels is not as dense in the area where this type of fat occurs, as it is with visceral fat. Another reason, which is related to degree of vascularization, is that subcutaneous fat is farther away from the portal vein than visceral fat. As such, it has to travel a longer distance to reach the main “highway” that will take it to other tissues (e.g., muscle) for use as energy.
In terms of health, excess subcutaneous fat is not nearly as detrimental as excess visceral fat. Excess visceral fat typically happens together with excess subcutaneous fat; but not necessarily the other way around. For instance, sumo wrestlers frequently have excess subcutaneous fat, but little or no visceral fat. The more health-detrimental effect of excess visceral fat is probably related to its proximity to the portal vein, which amplifies the negative health effects of excessive pro-inflammatory hormone secretion. Those hormones reach a major transport “highway” rather quickly.
Even though excess subcutaneous body fat is more benign than excess visceral fat, excess body fat of any kind is unlikely to be health-promoting. From an evolutionary perspective, excess body fat impaired agile movement and decreased circulating adiponectin levels; the latter leading to a host of negative health effects. In modern humans, negative health effects may be much less pronounced with subcutaneous than visceral fat, but they will still occur.
Based on studies of isolated hunger-gatherers, it is reasonable to estimate “natural” body fat levels among our Stone Age ancestors, and thus optimal body fat levels in modern humans, to be around 6-13 percent in men and 14–20 percent in women.
If you think that being overweight probably protected some of our Stone Age ancestors during times of famine, here is one interesting factoid to consider. It will take over a month for a man weighing 150 lbs and with 10 percent body fat to die from starvation, and death will not be typically caused by too little body fat being left for use as a source of energy. In starvation, normally death will be caused by heart failure, as the body slowly breaks down muscle tissue (including heart muscle) to maintain blood glucose levels.
References:
Arner, P. (2005). Site differences in human subcutaneous adipose tissue metabolism in obesity. Aesthetic Plastic Surgery, 8(1), 13-17.
Brooks, G.A., Fahey, T.D., & Baldwin, K.M. (2005). Exercise physiology: Human bioenergetics and its applications. Boston, MA: McGraw-Hill.
Fleck, S.J., & Kraemer, W.J. (2004). Designing resistance training programs. Champaign, IL: Human Kinetics.
Taubes, G. (2007). Good calories, bad calories: Challenging the conventional wisdom on diet, weight control, and disease. New York, NY: Alfred A. Knopf.
Labels:
adiponectin,
body fat,
leptin,
research,
tumor necrosis factor-alpha
Monday, October 23, 2023
The Friedewald and Iranian equations: Fasting triglycerides can seriously distort calculated LDL
Standard lipid profiles provide LDL cholesterol measures based on equations that usually have the following as their inputs (or independent variables): total cholesterol, HDL cholesterol, and triglycerides.
Yes, LDL cholesterol is not measured directly in standard lipid profile tests! This is indeed surprising, since cholesterol-lowering drugs with negative side effects are usually prescribed based on estimated (or "fictitious") LDL cholesterol levels.
The most common of these equations is the Friedewald equation. Through the Friedewald equation, LDL cholesterol is calculated as follows (where TC = total cholesterol, and TG = triglycerides). The inputs and result are in mg/dl.
LDL = TC – HDL – TG / 5
Here is one of the problems with the Friedewald equation. Let us assume that an individual has the following lipid profile numbers: TC = 200, HDL = 50, and TG = 150. The calculated LDL will be 120. Let us assume that this same individual reduces triglycerides to 50, from the previous 150, keeping all of the other measures constant with except of HDL, which goes up a bit to compensate for the small loss in total cholesterol associated with the decrease in triglycerides (there is always some loss, because the main carrier of triglycerides, VLDL, also carries some cholesterol). This would normally be seen as an improvement. However, the calculated LDL will now be 140, and a doctor will tell this person to consider taking statins!
There is evidence that, for individuals with low fasting triglycerides, a more precise equation is one that has come to be known as the “Iranian equation”. The equation has been proposed by Iranian researchers in an article published in the Archives of Iranian Medicine (Ahmadi et al., 2008), hence its nickname. Through the Iranian equation, LDL is calculated as follows. Again, the inputs and result are in mg/dl.
LDL = TC / 1.19 + TG / 1.9 – HDL / 1.1 – 38
The Iranian equation is based on linear regression modeling, which is a good sign, although I would have liked it even better if it was based on nonlinear regression modeling. The reason is that relationships between variables describing health-related phenomena are often nonlinear, leading to biased linear estimations. With a good nonlinear analysis algorithm, a linear relationship will also be captured; that is, the “curve” that describes the relationship will default to a line if the relationship is truly linear (see: warppls.com).
The Iranian equation yields high values of LDL cholesterol when triglycerides are high; much higher than those generated by the Friedewald equation. If those are not overestimations (and there is some evidence that, if they are, it is not by much), they describe an alarming metabolic pattern, because high triglycerides are associated with small-dense LDL particles. These particles are the most potentially atherogenic of the LDL particles, in the presence of other factors such as chronic inflammation.
In other words, the Iranian equation gives a clearer idea than the Friedewald equation about the negative health effects of high triglycerides. You need a large number of small-dense LDL particles to carry a high amount of LDL cholesterol.
An even more precise measure of LDL particle configuration is the VAP test; this post has a discussion of a sample VAP test report.
Reference:
Ahmadi SA, Boroumand MA, Gohari-Moghaddam K, Tajik P, Dibaj SM. (2008). The impact of low serum triglyceride on LDL-cholesterol estimation. Archives of Iranian Medicine, 11(3), 318-21.
Yes, LDL cholesterol is not measured directly in standard lipid profile tests! This is indeed surprising, since cholesterol-lowering drugs with negative side effects are usually prescribed based on estimated (or "fictitious") LDL cholesterol levels.
The most common of these equations is the Friedewald equation. Through the Friedewald equation, LDL cholesterol is calculated as follows (where TC = total cholesterol, and TG = triglycerides). The inputs and result are in mg/dl.
LDL = TC – HDL – TG / 5
Here is one of the problems with the Friedewald equation. Let us assume that an individual has the following lipid profile numbers: TC = 200, HDL = 50, and TG = 150. The calculated LDL will be 120. Let us assume that this same individual reduces triglycerides to 50, from the previous 150, keeping all of the other measures constant with except of HDL, which goes up a bit to compensate for the small loss in total cholesterol associated with the decrease in triglycerides (there is always some loss, because the main carrier of triglycerides, VLDL, also carries some cholesterol). This would normally be seen as an improvement. However, the calculated LDL will now be 140, and a doctor will tell this person to consider taking statins!
There is evidence that, for individuals with low fasting triglycerides, a more precise equation is one that has come to be known as the “Iranian equation”. The equation has been proposed by Iranian researchers in an article published in the Archives of Iranian Medicine (Ahmadi et al., 2008), hence its nickname. Through the Iranian equation, LDL is calculated as follows. Again, the inputs and result are in mg/dl.
LDL = TC / 1.19 + TG / 1.9 – HDL / 1.1 – 38
The Iranian equation is based on linear regression modeling, which is a good sign, although I would have liked it even better if it was based on nonlinear regression modeling. The reason is that relationships between variables describing health-related phenomena are often nonlinear, leading to biased linear estimations. With a good nonlinear analysis algorithm, a linear relationship will also be captured; that is, the “curve” that describes the relationship will default to a line if the relationship is truly linear (see: warppls.com).
The Iranian equation yields high values of LDL cholesterol when triglycerides are high; much higher than those generated by the Friedewald equation. If those are not overestimations (and there is some evidence that, if they are, it is not by much), they describe an alarming metabolic pattern, because high triglycerides are associated with small-dense LDL particles. These particles are the most potentially atherogenic of the LDL particles, in the presence of other factors such as chronic inflammation.
In other words, the Iranian equation gives a clearer idea than the Friedewald equation about the negative health effects of high triglycerides. You need a large number of small-dense LDL particles to carry a high amount of LDL cholesterol.
An even more precise measure of LDL particle configuration is the VAP test; this post has a discussion of a sample VAP test report.
Reference:
Ahmadi SA, Boroumand MA, Gohari-Moghaddam K, Tajik P, Dibaj SM. (2008). The impact of low serum triglyceride on LDL-cholesterol estimation. Archives of Iranian Medicine, 11(3), 318-21.
Subscribe to:
Posts (Atom)